Shematic.net

Теорема спектральной чувствительности

Теорема спектральной чувствительности

О. Капраль

Если в спектре сигналов с n-ным количеством гармоник значение i-той гармоники больше на удвоенную величину порога чувствительности от любой другой гармоники, то величина корреляционной функции между спектром и смещенным спектром пропорциональна относительной скорости объекта, что излучает этот спектр.

В общем виде теорема спектральной чувствительности определяет величину смещения спектра при относительной скорости объекта, что излучает частоты, или сигнал с некоторым количеством гармонических составляющих. Смещение спектра называется смещение Допплера.

Относительная скорость пропорциональна величине смещения между і-той гармоникой сигнала и і-той гармоникой смещенного спектра. А величину смещения можно определить корреляционной функцией между ними. При определении (измерении) величины смещения принимаются некоторые критерии:

– і-тая и к-тая гармоника – периодические сигналы;
– сигналы на промежутке периода являются непрерывными функциями;
– за порог чувствительности принимается значение шумов на входе приемных устройств или преобразователей.

Для дискретных сигналов теорему спектральной чувствительности можно сформулировать:

Если в спектре сигналов с N-ным количеством гармоник значение i-той гармоники больше, или равно любой другой гармонике на две единицы, то величина корреляционной функции между спектром и смещенным спектром пропорциональна относительной скорости объекта, излучающего этот спектр.

В аналоговых устройствах порог чувствительности определяется величиной шумов на входе, или соотношением сигнал/шум. Величина шумов, как правило, рассчитывается, или измеряется интегральным значением в соответствующей полосе частот. Для оценки распределения мощности шума по частотам используется спектральная плотность мощности шума и определяется как предел отношения мощности шума к полосе частот, которая еще называется интенсивностью шумов. Спектральная плотность мощности шума почти всегда постоянна от нулевых до высоких частот. Преобразователи аналоговых сигналов в цифровую характеризуются единицей младшего разряда, в масштабном значении приравнивается к величине максимального значения шумов на входе измерительных устройств.

Временная диаграмма на рис. 1 отражает мгновенное значение амплитуд і-той гармоники спектра, любой другой к-той гармоники и шумов на входе приемников, измерительных устройств, преобразователей.

Рис. 1. Мгновенное значение максимальных амплитуд гармонических составляющих сигнала и шумов.

Практически невозможно измерить задержку между і-той гармоникой спектра и і-той гармоникой смещенного спектра. Для этого используют гармоничный, или спектральный анализ.

Пусть входной сигнал состоит из набора периодических сигналов, которые описываются функциями:

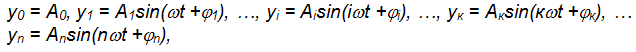
где 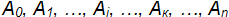– амплитуды периодических функций и их частоты 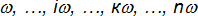связанные с периодом T соотношением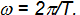

Тогда входной сигнал можно описать как функцию, состоящую из суммы, или набора простых гармонических составляющих:

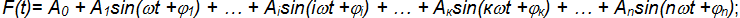
для которого справедливо преобразование:

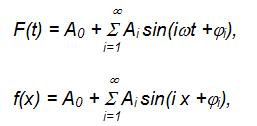
где 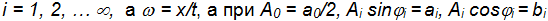может быть разложена в ряд Фурье и записана в виде:

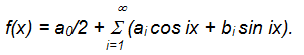
В практике спектрального анализа используется быстрое преобразование Фурье и дискретное преобразование Фурье, при i = 1, 2, … n пользуются приблизительным вычислением значений функций:

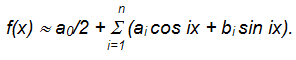
Рис. 2. Гармонические составляющие входного сигнала и смещенного спектра после преобразования Фурье.

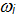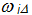На рис. 2 отображено мгновенное значение амплитуды і-той гармоники входного сигнала и смещенного спектра в частотном отображении при i = 1, 2, … n, где - частота і-той гармоники, а – частота і-той гармоники смещенного спектра.

Из рис. 2 видно, что для определения смещения частоты достаточно одной гармонической составляющей в входном сигнале, а амплитудное значение любой другой гармоники можно приравнять к величине шумов на входе преобразовательных устройств.

Запишем преобразование Фурье в общем виде:

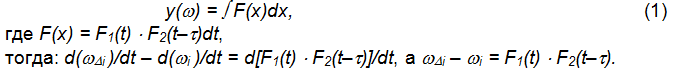
При спектральном анализе используется метод накопления, или суммирования мгновенных значений спектральных составляющих сигнала с определенным количеством гармоник и усреднений, і = 1, 2 ... N, что дает возможность увеличить выходной сигнал в N раз, а случайные составляющие в 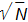и улучшить соотношение сигнал/шум на выходе преобразователей.

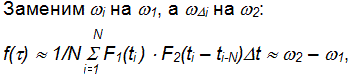
где 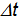– определяет чувствительность устройства на изменение частоты, а взаимокорреляцийная функция – величину относительного смещения спектра в принятых сигналах. Величина 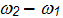называется Допплеровским смещением частоты и используется для определения скорости объекта в пассивной и активной гидролокации и радиолокации.

добавлено 24.04.19 12:09:11 | просмотрено 2160 раз