Shematic.net

Логическое исправление ошибки

В статье “Восстановление потерянной информации” рассмотрен вопрос о восстановлении визуальной информации при потере из-за наличия помех. Наиболее эффективным методом восстановления информации есть накопление данных. Но этот метод требует усложнения аппаратных устройств и алгоритмов обработки данных, в свою очередь и значительных временных затрат. Аналоговые сигналы от датчиков и устройств, в основном, преобразуется в цифровые коды и на большие расстояния передается в цифровом виде (при смене среды передачи сигнал модулируется). Цифровая передача, в свою очередь, повышает защищенность от случайных и систематических помех. Большая интеграция элементов на одном кристалле также повышает помехозащищенность сигналов. Но ситуация потери информации возникает в случае понижения уровня принимаемого сигнала до уровня помехи, или некоторого порога уровня логического “0”, или логической “1”. Преобразование простого NRZ-кода в код Грея в некоторой степени повышает помехозащищенность передачи данных подобно дельта - модуляции, когда две последовательные цифры отличаются на одну единицу (при дельта - модуляции на минимальное дельта значение величины сигнала). Преобразование двоичной системы счисления в код Хемминга произвело к целому семейству протоколов передачи данных.

Наибольшим быстродействием является параллельная передача данных и наиболее защищенными от помех – параллельные каналы. Но резервирование целых устройств, в некоторых случаях приводит к увеличению затрат, аппаратуры, потребления.

В данной статье рассмотрен алгоритм исправления ошибки в одном разряде цифровой последовательности, независимо это параллельная, или последовательная передача данных, или цифровая обработка, а количество разрядов не ограничено. Например, передача данных от регистра к регистру, от регистра к счетчику, или к АЛУ и т. п.

Из двух двоичных параллельных последовательностей, например, 1101 и 1001 невозможно определить “истину” “1”, или “0” в третьем разряде (младшие разряды справа), ибо мы можем сказать, что в первой последовательности, из-за помехи, “0” изменился на “1”, также можно определить, что во второй последовательности в том же разряде “1” изменилась на “0”. Для исправления ошибки необходимо ввести еще одну последовательность: 1101, 1001, 1101. Тогда логическое исправление ошибки можно представить формулой:

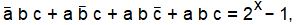
где х = 0, 1, 2, 3… – номер разряда в цифровой двоичной последовательности.

То есть, если два совпадения – это “истина”, если “0” и “0”, значение сигнала – “0”, и если “1” и “1” значение сигнала – “1”. На рис. 1 изображена схема, реализующая данный алгоритм.

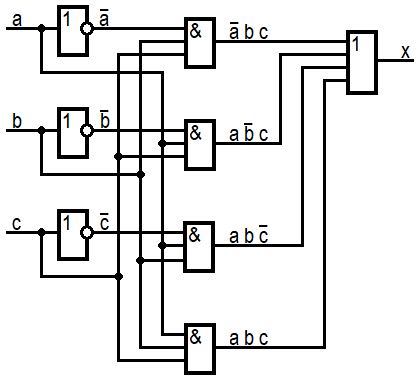
Рис. 1. Логическое исправление ошибки.

Применив преобразования к вышеуказанной формуле, схему на рис. 1 можно упростить, такая схема изображена на рис. 2:

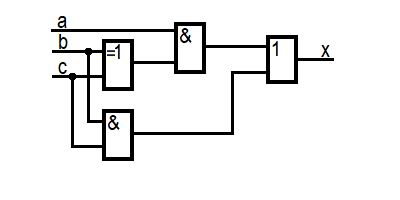
Рис. 2. Упрощенная схема логического исправления ошибки.

Логическое исправление ошибки может применяться в наиболее ответственных каналах, или местах каналов при передаче данных цифровым способом, например при экстремальных условиях среды, повышенных, или пониженных температурах, при повышенных уровнях радиации, при повышенных уровнях помех и др.

добавлено 02.03.21 11:53:13 | просмотрено 4620 раз